[패턴인식] SVM
SVM - Support Vector Machines의 개념에 대해서만 작성해보았다.
SVM이란
- Support vector를 기준으로 margin을 최대화하는 결정 경계선으로 분류하는 방법
Density 기반의 분류 방법
- SVM은 샘플 데이터들의 밀도를 기준으로 분류하지 않으며, 서포트 벡터만으로 결정 경계선(또는 면)을 결정함
- Density 기반 분류기의 예: 베이시언 분류기, KNN 분류기 등
SVM의 특징
- SVM은 샘플들의 밀도를 기준으로 삼지 않기 때문에, 샘플 데이터가 추가되더라도 서포트 벡터가 변하지 않으면 결정 경계가 변하지 않음
- 샘플 데이터의 밀도와 관계없이 margin을 최대화하는 경계선을 찾기 때문에 분류의 일반화 능력이 뛰어남
- 신경망 학습을 통한 분류는 성능이 뛰어나더라도 margin 최대화를 보장하지 못하는 경우가 있음
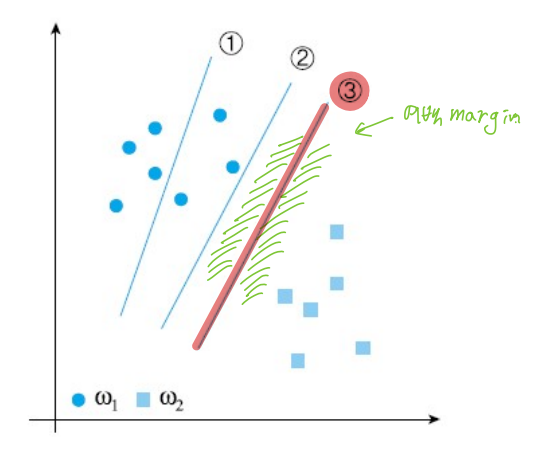
위 그림에서 3번 경계선과 직각으로 가장 가까운 거리의 샘플(벡터)이 서포트 벡터임
또한 margin은 결정 경계선과 서포트 벡터 간의 거리의 두 배 길이
→ (결정 경계선과 서포트 벡터 간의 거리) X 2 = margin
선형 SVM
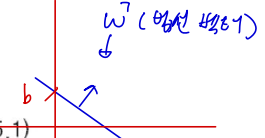
수학적 표현
특징 공간에서 선형 결정 경계선 \( d(\mathbf{x}) \)를 기준으로 샘플 데이터들이 분류됨
\[d(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + b = 0\]샘플 데이터들은 아래 조건에 따라 분류됨
- \( d(\mathbf{x}) > 0 \) 또는 \( d(\mathbf{x}) < 0 \)
임의의 샘플 x로부터 초평면까지의 거리
샘플 \( x \)가 결정 경계선으로부터 얼마나 떨어져 있는지 계산하기 위해, 다음 식을 사용함
\[h = \frac{\lvert d(\mathbf{x}) \rvert}{\lVert \mathbf{w} \rVert}\]여기서 \( x \)가 서포트 벡터라면, \( 2h \)가 margin 값이 됨
SVM으로 최적의 결정 경계를 찾기
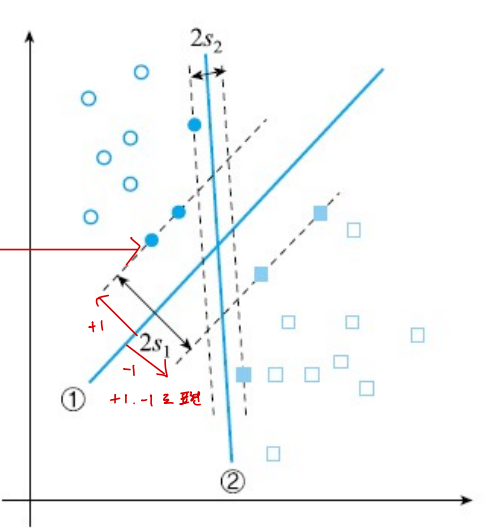
위 그림에서 SVM 방식을 사용하여 분류한 결과, SVM은 여백을 최대화하는 분류 방식이므로 결정 경계선 1번이 더 적합해 보임
그럼 분류 문제가 주어졌을 때 어떻게 1번 경계선을 찾는지?
- 여백을 가장 크게 하는 결정 경계선의 방향을 찾아야 함. 즉, \( \mathbf{w} \)를 찾아야 하며, 이는 최적화 문제로 해결할 수 있음
최적화 문제
- 최적화 문제는 margin크기에 반비례하는 하이퍼플레인의 normal 방향 벡터인 ** w를 최소화하는 문제 **이며, 라그랑제 승수를 푸는 문제로 최적화된다.
최적화 문제를 푸는 부분은 양이 많아 작성하지 않을 예정임