[패턴인식] Maximum Likelihood Estimation
목차
Maximum Likelihood Estimation (MLE)
MLE (Maximum Likelihood Estimation)은 주어진 데이터 $ X $를 통해 매개변수 $ \Theta $를 추정하는 모수적 추정 방법이다.
목표:
- 주어진 $ X $를 발생시켰을 가능성이 가장 높은 매개변수 $ \Theta $를 찾는다.
- 주어진 $ X $에 대해 가장 큰 우도를 갖는 $ \Theta $를 찾는다.
정규 분포를 가정할 경우, 매개변수는 평균 $ \mu $과 분산 $ \Sigma $ (공분산 행렬)이다.
최대 우도 추정 단계
1. 우도가 최대가 되는 Θ 찾기
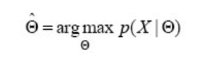
2. 독립적이고 동일하게 분포된 샘플 가정
모든 $ X $ 샘플이 독립적으로 추출되었다고 가정하면, 우도는 다음과 같이 표현된다.
iid (Independent and Identically Distributed)
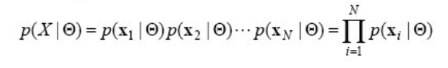
3. 로그 우도 함수
우도에 로그를 취하면 곱을 합으로 나타낼 수 있다.
\[\log L(\Theta) = \sum_{i=1}^{N} \log P(x_i|\Theta)\]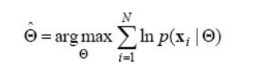
4. 우도 최대화
우도의 최대값을 찾기 위해 $ \Theta $에 대해 미분한 값을 0으로 둔다.
\[\frac{\partial \log L(\Theta)}{\partial \Theta} = 0\]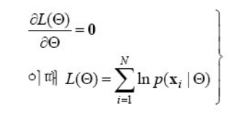
정규 분포 가정 시 MLE
가정
-
가정 1: $ X $가 정규 분포에서 추출되었다.
(매개변수는 평균 $ \mu $과 분산 $ \Sigma $ (공분산 행렬)) -
가정 2: 공분산 행렬은 이미 알고 있다.
(공분산 행렬 $ \Sigma $를 상수로 간주)
유도 1: 평균 $ \mu $ 추정
식의 도함수를 0으로 두었을 때,

최적의 매개변수 $ \mu $는 샘플들의 평균 벡터로 표현된다.
\[\mu = \frac{1}{N} \sum_{i=1}^{N} x_i\]유도 2: 공분산 행렬 $ \Sigma $ 추정
가정 2를 다음과 같이 변경한다:
- 가정 2: 평균은 이미 알고 있다.
(평균 벡터 $ \mu $는 상수)
그럼, 공분산 행렬 $ \Sigma $만 변수로 생각하면 되므로, $ \Sigma $에 대해 미분하고 0으로 두면,
\[\Sigma = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)(x_i - \mu)^T\]샘플 개수가 많아지면 $ \frac{1}{N-1} $와 $ \frac{1}{N} $의 차이는 무시될 수 있다.
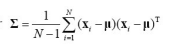
결론
정규 분포를 가정하고 MLE 방법으로 최적의 매개변수를 구하면, 이는 실제 샘플들의 평균과 공분산과 동일함을 알 수 있다. MLE 방법은 사전 확률을 전혀 고려하지 않고 데이터를 통해 매개변수를 추정하는 방법인데, 다음으로 소개할 MAP (Maximum A Posteriori) 방법은 사전 확률을 고려하여 매개변수를 추정하는 방법이다.