[패턴인식] 신경망

신경망

신경망 특성

• 학습 가능
• 뛰어난 일반화 능력
• 병렬 처리 가능
• 현실적 문제에서 우수한 성능
• 다양한 문제 해결 도구 (분류, 예측, 함수 근사화, 합성, 평가 등)

single layer 형태

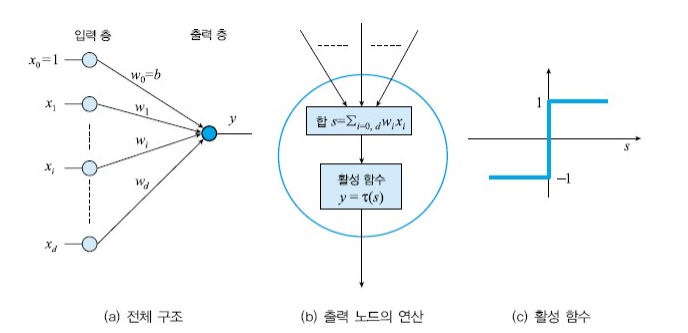
1개의 레이어를 가진 구조는 선형 분류만 가능하다. 비선형 분류기를 만들기 위해서는 2개 이상의 Layer가 필요. 2개 이상의 레이어 = Multi layer

패턴 인식 관점에서 알고리즘은 어떻게 설계되는지

1단계 : 분류기 구조 정의 (수학식 정의)
2단계 : 비용함수 \(J(\Theta)\) 정의 → 신경망 구조 정의
3단계 : \(J(\Theta)\) 최적화 → forward 계산, Backpropagation, Gradient descent 등 학습 과정을 통해 최적의 파라미터를 찾는다.

분류기 품질을 측정하는 비용함수

\(J(\Theta) = \sum_{\{x_k\} \in Y} (-t_k) (\mathbf{w}^T \mathbf{x_k} + b)\)

• ( Y ): (오분류된 샘플 집합 또는 모든 샘플)
• Y가 공집합이면 J(Θ)=0

• Y	가 클수록 J(Θ) 값이 증가

Gradient descent를 그림으로 표현하면

\[-\frac{\partial}{\partial \Theta}\]

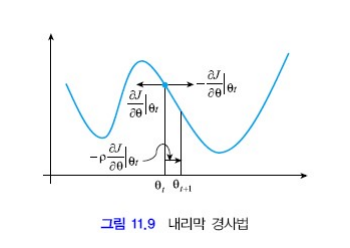
위 방향으로 가야 minimum을 찾을 수 있음. Gradient Descent는 비용 함수의 기울기를 따라 최소값을 찾는 방식으로 진행되며, 항상 전역 최소값을 찾을 수 있는 것은 아니다.

XOR 문제와 같이 선형 분류가 불가능한 문제는 다중 레이어를 이용한다고 했다.

• 멀티 레이어를 이용한다는 것은 샘플 공간의 차원이 달라진다는 것을 의미 → 새로운 공간에서 분류한다.

멀티 레이어 구조 (Feed-Forward Multi Layer Perceptron : FFMLP)

• Input Layer와 Output Layer 사이에 하나의 Hidden Layer가 존재하고 있다.
• 하나가 아닌 수많은 Hidden Layer를 가지는 경우 DNN이라고 부른다.

forward 계산, Backpropagation

역전파 계산 과정을 블로그에서 상세히 설명하기는 곤란하여 생략함.

• 오류 역전파 알고리즘의 계산 복잡도: Θ((d+m)pHN)
  • H는 hidden layer의 노드 수와 관련
  • 많은 시간 소요. 예) MNIST 필기 숫자 데이터베이스는 N=60000
• 시간 복잡도 Θ((d+m)p)
  • 전체 샘플 갯수 N에 무관하여 빠름.

학습을 언제 종료해야 하는지

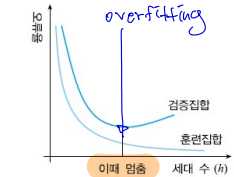
일정 수준 이상 학습이 진행되면 Training set에 overfitting되어 Test set의 오류율이 상승하기 시작한다. 이를 방지하기 위해 학습을 조기에 종료하는 방법(Early Stopping)을 사용할 수 있다.